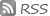뫼비우스의 띠 Möbius Strip
[개념] - 수학의 기하학과 물리학의 역학이 관련된 곡면
- 안팎의 구별이 없는 2차원 도형
[특징] - 어느 지점에서나 띠의 중심을 따라 이동하면 출발한 곳과 정반대 면에 도달한다.
- 계속 나아가 두 바퀴를 돌면 처음 위치로 돌아온다.
1. 유클리드 (Euclid, BC 300년경)
① 고대 그리스의 수학자
② 수학 체계 '유클리드 기하학(Euclidean geometry)' 구축
③ 기하학에 관해 처음 체계적으로 논의한 학자
④ 직관적으로 인지되는 공리를 참으로 가정, 가정한 것들로부터 연역적으로 명제 도출
⑤ 포괄적 추론과 논리를 통해 수학적 명제의 성립을 증명한 최초의 인물
2. 패러다임의 변화
① 유클리드 기하학이 2천 년 간 진리로 간주
② 19세기 후반 '비유클리드 기하학'-유클리드 기하학으로는 설명할 수 없는 기하학적 관념- 등장
③ 2차원의 평면에서는 통용되었던 원리가 3차원의 입체에서는 적용되지 않는 문제 발생
④ 예제
A. 축구공 위에 그은 직선은 결과적으로 직선이 아닌 곡선이 된다.
B. 삼각형의 내각의 합은 180°이다.
a. 평면에서는 '참'이 된다. 그러나,
b. 축구공 안쪽 면에 그린 삼각형의 내각의 합은 180° 미만
c. 축구공 바깥 면에 그린 삼각형의 내각의 합은 180° 초과
3. 뫼비우스의 띠
① 독일의 수학자 겸 천문학자 뫼비우스(August Ferdinand Möbius, 1790~1868)에 의해 고안
② 차원의 초월 개념을 시각적으로 확인시켜준 도형
③ 유클리드 기하학의 한계 극복
④ 2차원의 평면을 3차원화한 곡면
⑤ 2차원과 3차원의 성질을 동시에 포함
⑥ 현대 첨단산업에서의 활용
A. 뫼비우스 띠처럼 꼬인 물체의 잘 찢기는 부분을 예측케 하는 수단
B. 화학, 양자물리학, 나노테크놀로지를 이용한 신약 구조의 연구와 개발
※ 개념어사전 | 남경태 저 | 도서출판들녘
※ 위키백과
쾌도난마 개념어 MONZAQ
'쾌도난마 개념어' 카테고리의 다른 글
| 미장센 Mise en Scéne (0) | 2013.05.20 |
|---|---|
| 격률 格率 maxim (0) | 2013.05.20 |
| 참칭 僭稱 (0) | 2013.05.18 |
| 제로섬 zero sum (0) | 2013.05.18 |
| 엄숙주의 Rigorism [ríɡərìzm] (0) | 2013.05.18 |